Code de numération : Révisions⚓
En mathématique, il est possible de compter de différentes façons. Il existe la base décimale, qui est la base la plus communément répandue, celle que nous utilisons tous les jours pour compter. Il est aussi possible de compter en base 2 (binaire), en base 8 (octal) et en base 16 (hexadécimal). D'autres bases existent, en fait une infinité, mais les bases précédemment citées sont celles qui sont le plus souvent utilisées en électronique et en informatique.
Systèmes de numération pondérés
Les bases utilisées pour compter sont toutes des systèmes de numération pondérés, cela siginfie que le système comprend :
une base,
des symboles,
un poids pour chaque chiffre du nombre selon leur rang.
Système décimal
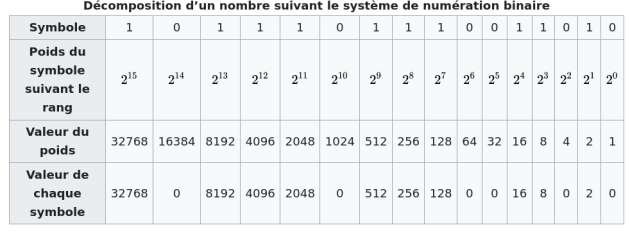
Système binaire
Système hexadécimal
Le système hexadécimal correspond à la base 16, il est composé :
de 16 symboles : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F,
d’un poids qui correspond aux puissances de 16.
L'utilisation de symbole de lettres latines nous est imposé par le fait que les symboles chiffres sont limités à un nombre de 10, de ce fait, et pour continuer le poids du symbole :
A vaut 10
B vaut 11
C vaut 12
D vaut 13
E vaut 14
F vaut 15
Donc 73 D A (16 ) = 29675 (10 )
Tout comme en octal, on retrouve des valeurs identique entre les poids des rangs en système hexadécimal et les poids des rangs binaires.
On va donc trouver un système très simple pour passer d'une base hexadécimal vers une base binaire.
Changement de base
On procède par divisions successives du nombre par la base dans laquelle on veut l'écrire.
Le nombre converti commence par le dernier reste trouvé, les autres chiffres viennent des autres restes lus en sens inverse.
Exemple
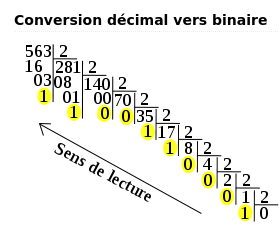
Sur l'image ci-dessus, c’est la conversion du nombre 563 en son équivalent en binaire : le reste d'une division par deux ne peut être que 0 ou 1. On obtient donc :
563 ( 10 ) = 1000110011 ( 2 )
Conversion en hexadécimal :
On reprend (évidemment) le même principe de division successives ("incrémental") sauf que, comme le laisse supposer "hexa", cette fois on dispose d'une base 16. Comme nos chiffres (le mot bit) est parfois emprunté au binaire, celui de "chiffre" est préférable) usuels ne peuvent exprimer que dix valeurs il fallait trouver une parade. Celle choisie consiste à utiliser des lettres. Nous utiliserons donc A,B,C,D,E et F, respectivement 10, 11, 12, 13, 14 et 15.
Comme précédemment un "piège mental" est que 0 compte pour une unité, ainsi :
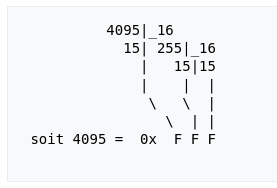
On précède généralement un digit hexadécimal de "0x" pour notifier que l’on utilise l'hexadécimal: en effet si le nombre évoqué est pas exemple 0x443, cela donne 1091 en décimal ce qui diffère quelque peu de 443 vous en conviendrez.
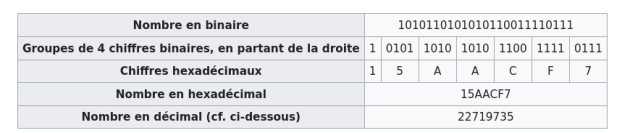
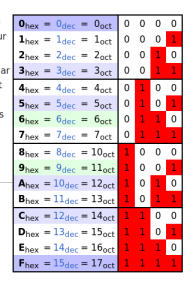
La conversion de binaire en hexadécimal se fait en regroupant les chiffres (les bits) quatre par quatre, ou inversement en remplaçant chaque chiffre hexadécimal par 4 chiffres binaires, du fait que 16 = 24. La justification de la conversion d'hexadécimal en binaire est donnée pour des nombres de 0 à 255 qui s'écrivent avec au plus deux chiffres hexadécimaux ou 8 chiffres binaires, :
Tableau de synthèse :
Exercices :
Exercice 1 :
Conversion Binaire décimal :
0110
01110010
11111000
1111
01010101
Exercice 2 :
Conversion décimal binaire puis hexa:
34
255
4034
148
Exercice 3 :
Conversion décimale binaire :
45
233
5
24