Rappels en électricité⚓
Exemple de schéma électrique
Simulation sur CircuitJS
Mesure de l'intensité du courant et de la tension
Dipôles
Un dipôle électrique est un composant électrique comportant deux bornes (exemple : Lampes, Piles, résistances).
On distingue 2 types de dipôle :
Les générateurs qui produisent un courant électrique
Les récepteurs qui reçoivent un courant.
NB : Par convention dans un schéma électrique on flèche le courant et la tension ainsi :
Attention : Le sens des flèches
La tension \(U_{AB}\) doit pointer sur le point A. La tension \(U_{BA}\) doit pointer sur B. \(U_{AB} = - U_{BA}\)
Quelques exemples
Exercice 1
Flécher les tensions \(U_{AB}, U_{CB}, U_{CD}, U_{DI}, U_{EH}, U_{GF}, U_{AJ}\)
Entourer en rouge les dipôles générateurs et en vert les dipôles récepteurs.
Flécher le courant dans chaque dipôle.
Loi des mailles et la loi des nœuds
Dans un schéma électrique les dipôles sont reliés par des branches ou fils. L'interconnexion d'au moins trois fils est représentée par un nœud. Deux dipôles peuvent être connectés soit en série soit en dérivation. La loi des mailles et la loi des nœuds présentées ci-dessous permettent une analyse directe d'un schéma électrique complexe :
La loi d'ohm
Le composant représenté dans le cadre orange est une résistance dont les bornes sont connectées au générateur. Ce générateur impose une tension constante notée U (en Volt) aux bornes de la résistance. Un courant électrique (mouvement d'électrons) noté I (en A) circule de la borne + du générateur, traverse la résistance et retourne vers la borne - du générateur.
La tension U et le courant peuvent être déduit l'un de l'autre si on connaît la valeur de la résistance (en Ohm) par la loi d'ohm :
U = R I
La résistance R (en Ω) est une propriété caractérisant la «facilité » des électrons à circuler dans un matériaux.
Cas particuliers :
Exercice 2
Avec un générateur de 9V et une résistance de R=1 kΩ, calculer la valeur du courant I en A puis en mA:
Que se passe-t-il si on branche une résistance nulle aux bornes d'un générateur ?
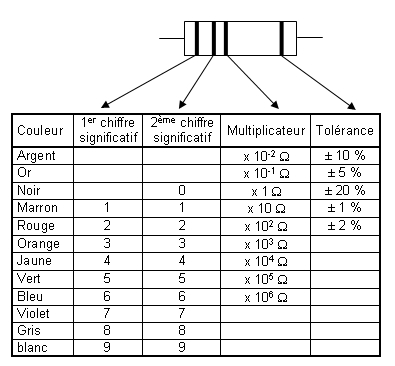
Code couleur
Montage série des résistances
On peut montrer que le montage ci-dessus est équivalent à celui ci -contre :
Avec \(Req = R1 + R2 + R3 + R4 + R5\)
Montage parallèle des résistances
On montre que le montage ci-contre est équivalent à celui en dessous :
Avec Req :
montrer que pour N = 2 :
\(Req = \frac{R1 \times R2}{R1 + R2}\)
Diviseur de tension :
On peut montrer que :
\(U_1 = U \frac{R_2}{R_1 + R_2}\)