LE FILTRAGE DES SIGNAUX⚓
Le filtrage sert à éliminer certaines fréquences présentes dans le signal d'entrée. On peut considérer un filtre comme étant une boite avec une entrée et une sortie.
Spectre
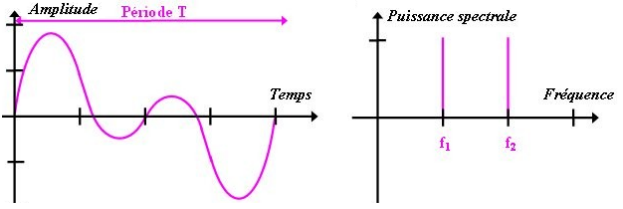
Il est pratique de visualiser les signaux en fonction de la fréquence et non en fonction du temps, c'est ce que l'on appelle le spectre.
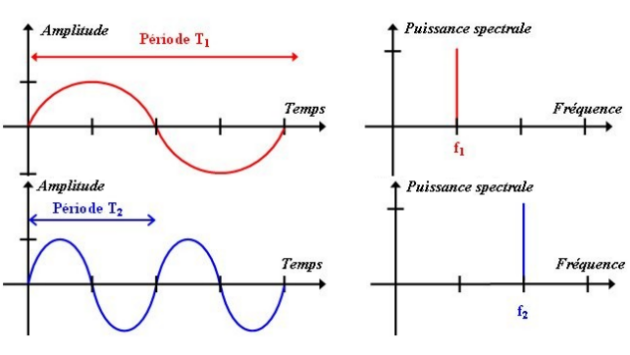
La courbe suivante résulte de la combinaison des deux fonctions précédentes est caractérisée par deux composantes périodiques. L'analyse spectrale permet de retrouver les deux fréquences du signal : f1 et f2.
En effet, un signal périodique est la somme d'une multitude de sinusoïdes, la figure ci-dessous montre comment on peut construire un signal carré à l'origine :
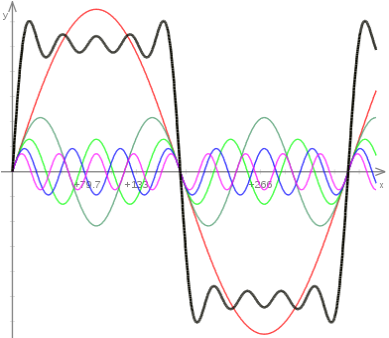
La somme des sinusoïdes de couleur donne le signal de couleur noire.
Le signal n'est pas tout à fait carré car il n'est construit qu'avec 5 sinusoïdes :
-le fondamental : qui a la même fréquence que le signal carré.
-les harmoniques : qui ont des fréquences multiples du fondamental.
Tracer son spectre ci-dessous :
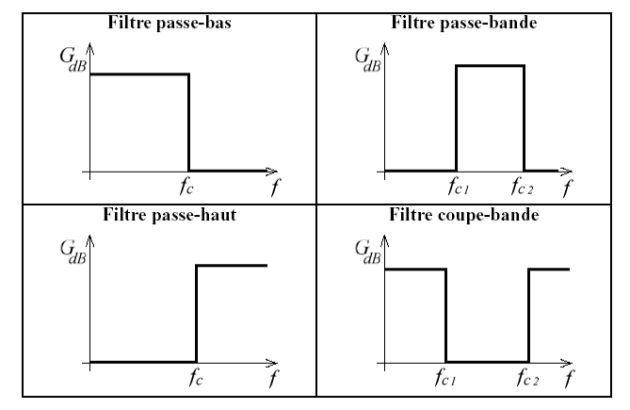
Types de filtre
Le gabarit d'un filtre indique les limites fréquentielles (fc : fréquence de coupure) que doit respecter le filtre
Filtrage d'un signal carré :
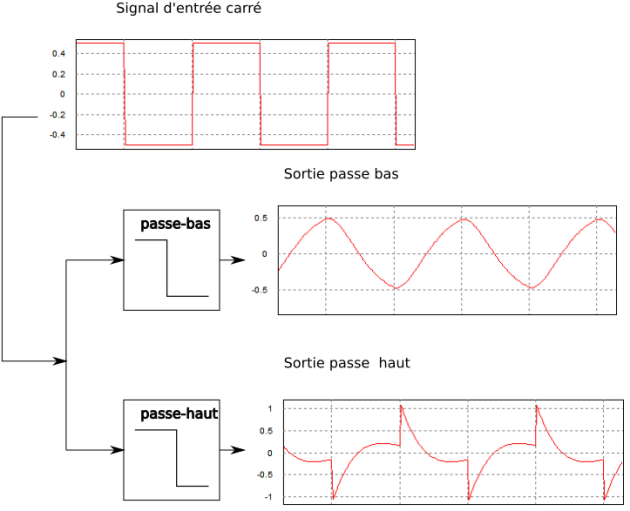
Filtrage passe bas : il ne laisse passer que le fondamental, une sinusoïde de même fréquence que le signal carré.
Filtrage passe haut : ce filtre ne réagit que lorsque le signal carré varie rapidement, ici sur les fronts (voir quand apparaissent les pointes)
Fonction de transfert
Les filtres sont des systèmes qui ont ce que l'on appelle des fonctions de transfert \(T\) en fonction de la fréquence \(f\), c'est le rapport entre l'amplitude du signal de sortie, \(S(f)\) sur celle du signal d'entrée \(E(f)\):
\(T(f) = S(f) / E(f)\)
Cette fonction de transfert T(f) est très souvent en traitement du signal audio exprimée en dB, on parle alors du Gain G(dB) :
\(G(dB) = 20 * \log (T) = 20 \log (S / E )\)
Par exemple, le filtre passe-bas a une fonction de transfert qui vaut 1 quand la fréquence est basse (\(f\) proche de zéro), ce qui veut dire que le signal de sortie vaut le signal d'entrée, alors que dans les hautes fréquences, la fonction de transfert tend vers 0 ce qui veut dire que le signal de sortie est fortement atténué par rapport au signal d'entrée.
Soit les 2 fonctions de transfert, une passe haut et l'autre passe bas à vous de trouver les fonctions de transfert :
Filtre : passe ___________________ | Filtre : passe _________________________________ |
Fonction de transfert : \(T(f) = \frac{kf}{(1+kf)}\) Que vaut T si f tends vers 0 ? _________________________________ Que vaut T si f tends vers l'infini ? _________________________________ Que vaut la sortie S _______________________________ | Fonction de transfert : \(T(f) = \frac{1}{(1+kf)}\) Que vaut T si f tends vers 0 ? _______________________________ Que vaut T si f tends vers l'infini ? ________________________________ Que vaut la sortie S ______________________________ |
Quel est le comportement de ce filtre aux basses fréquences ? ___________________________________ Quel est le comportement de ce filtre aux hautes fréquences ? ___________________________________ | Quel est le comportement de ce filtre aux basses fréquences ? _______________________________ Quel est le comportement de ce filtre aux hautes fréquences ? _________________________________ |
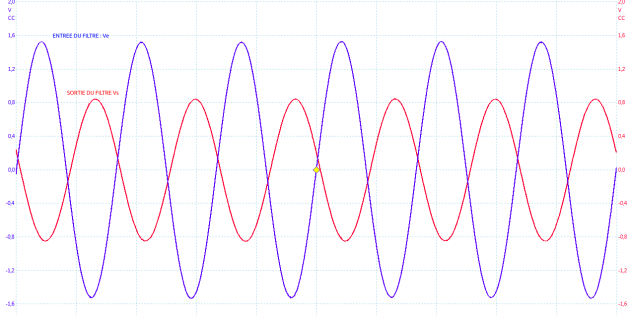
Calculer le transfert puis le gain du filtre en dB entre l'entrée et la sortie (signaux ci-dessus ):
RÉCEPTION RADIO
L'antenne d'une radio reçoit toutes les fréquences émises. Un filtre composé d'un condensateur et d'un bobine (ci-dessous) doit filtrer les signaux en ne gardant que la fréquence désirée.
Dans ce type de filtre, le condensateur \(C\) est variable, ce qui permet d'isoler une fréquence que l'on appelle fréquence de résonance \((f0)\).
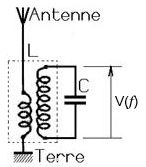
Quel type de filtre doit-on utiliser ?
Quelles sont ses caractéristiques ?
Voici un filtre électronique utilisé dans une radio, repérer la bobine et le condensateur.
Sachant que la fréquence voulue est \(864 KHz\) et que \(L\) vaut \(170 \mu H\) donner la valeur de \(C\) en Farad (F).
Relation entre \(f0\), \(L\) et\( C\) pour ce circuit :
\(f0 = \frac{1}{2 \pi \sqrt{LC}}\)
Représentation en échelle logarithmique
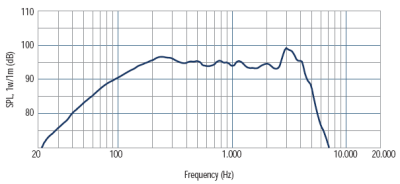
Pour représenter le comportement d'un haut parleur on étudie la puissance (ici en DB) en fonction de la fréquence. L'échelle habituellement utilisée est l'échelle logarithmique.
Une échelle logarithmique est particulièrement adaptée pour rendre compte des ordres de grandeur dans les applications. Elle montre sur un petit espace une large gamme de valeurs, à condition qu'elles soient non nulles et de même signe ce qui est le cas de la fréquence.
Quelle est la sensibilité SPL (en DB) du haut parleur à 200Hz ?
A quelle fréquence cette sensibilité est-elle max ?
Filtre RC
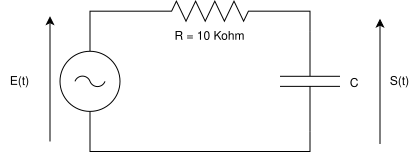
La fonction de transfert de ce filtre s'écrit :
\(T(f) = \frac{S(f)}{E(f)}=\frac{1}{\sqrt{1+(2*\pi R C f)^2}}\)
Que vaut T si f tend vers 0 ?
Que vaut alors la sortie S ?
Que vaut T si f tend vers l'infini ?
Que vaut alors la sortie S ?
On souhaite utiliser ce filtre pour filtrer un signal audio. Garder les signaux de la bande audio et supprimer les autres. La fréquence de coupure \(fc = 20kHz\) :
La fréquence de coupure est la valeur de la fréquence pour laquelle \(T(fc) = 1/\sqrt{2}\).
Calculer l'expression de cette fréquence de coupure en fonction des composants \(R\) et \(C\).
Calculer la Capacité du condensateur C (en pF) pour avoir \(fc=20kHz\)
Calculer pour les valeurs de f ci-dessous le transfert et gain en dB :
f(Hz) | 100 | 300 | 1000 | 10000 | 20000 | 30000 | 40000 | 80000 | 100000 |
T | |||||||||
G(dB) = 20 *log(T) |
Tracer la courbe de gain
