Exercices filtrage⚓
Filtre RC 2

La fonction de transfert de ce filtre s'écrit :
\(T(f) = \frac{Vs(f)}{Ve(f)}=\frac{2 \pi R C f}{\sqrt{ 1+ (2 \pi R C f) ²}}\)
Que vaut T si f tend vers 0 ?
Que vaut alors la sortie Vs ?
Que vaut T si f tend vers l'infini ?
Que vaut alors la sortie Vs ?
Que se passe-t-il à la fréquence de coupure : \(f = fc = \frac{1}{2 \pi RC}\), Que vaut \(T(fc)\) en dB ?
On souhaite utiliser ce filtre pour filtrer un signal audio. Garder les signaux de la bande audio et supprimer les autres. La fréquence de coupure \(fc = 20Hz\) :
Calculer la valeur de \(C\) avec \(R = 10 k \Omega\)
Calculer pour les valeurs de f ci-dessous le transfert et gain en dB :
f(Hz) | 1 | 10 | 20 | 50 | 100 | 200 | 1000 | 2000 | 20000 |
T | |||||||||
G = 20 log (T) |
Tracer la courbe de gain
Simulation Circuit JS Circuits -> Filtres passifs -> Filtre passe-haut (RC)
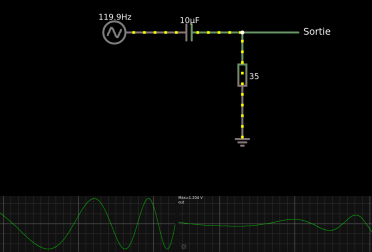
A partir d'un dessin vide (Menu : Circuits -> Circuit vide) démontrer les résultats ci-dessus.